We consider here the two-dimensional problem of scattering a time-harmonic incident field by a bounded sound soft obstacle D. Splitting up the total field into incident and scattered field, we have the following boundary value problem for the scattered field:
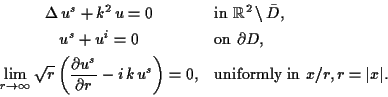
The problem can be solved very efficiently by making a combined double- and single-layer potential ansatz,
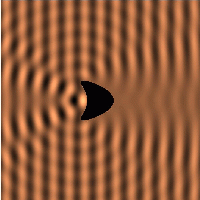
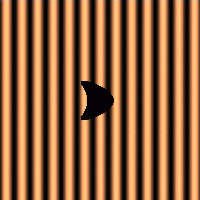
The images on the right-hand side show visualisations of the solution to this scattering problem for the case of a plane wave incident from the left. Each image shows the real part of the incident, scattered and total field computed with this method, respectively. Below you have the option of downloading an animation visualising the toatal field. Just click the button to start the animation.
Animated visualisation of the total field:
Incident field:
Scattered field:

Total field: