Scattering by a Diffraction Grating
 A diffraction grating problem is the problem of scattering a plane incident wave by a
periodic surface. We will here consider the case, when the total
field vanishes on the surface. This corresponds, for example, to a TE polarised
electromagnetic wave incident onto a perfectly conducting surface.
A diffraction grating problem is the problem of scattering a plane incident wave by a
periodic surface. We will here consider the case, when the total
field vanishes on the surface. This corresponds, for example, to a TE polarised
electromagnetic wave incident onto a perfectly conducting surface.
Mathematically, the problem is posed as a boundary value problem for the scattered
field in the unbounded domain above the periodic surface, which is given as the graph o
f a function f. The governing equation is the Helmholtz equation,
and the boundary condition is that the sum of scattered and incident field vanishes on f.
To ensure uniqueness of solution to the mathematic boundary value problems, the scattered field
will be assumed to be quasi-periodic, i.e. for some a > 0,
and, as a radiation condition, will be assumed to have an expansion of the form
for some
x2 > max f, where
 A further consequence of these assumptions is that the problem can be formulated
equivalently through a boundary integral equation that only involves an integral over
a single period and thus is finite. Thus the corresponding integral operator can
be shown to be compact.
A further consequence of these assumptions is that the problem can be formulated
equivalently through a boundary integral equation that only involves an integral over
a single period and thus is finite. Thus the corresponding integral operator can
be shown to be compact.
The images on this page show the incident and scattered fields for such a problem
involving a sinusoidal surface. The fields were computed by a numerical software package
implemented by the Brunel University Rough Surface Scattering group, based on an exponentially
convergent Nyström method for the solution of the boundary integral equation.
Below, you can view an animation of the total field for this problem using a Java
applet. Click the button to download the animation data and start viewing.
Page written and maintained by Tilo
Arens
last change: 24 July 2000
Mathematical formulae by latex2html
Java animation applet by Markus Kraft
and Tilo Arens
 A diffraction grating problem is the problem of scattering a plane incident wave by a
periodic surface. We will here consider the case, when the total
field vanishes on the surface. This corresponds, for example, to a TE polarised
electromagnetic wave incident onto a perfectly conducting surface.
A diffraction grating problem is the problem of scattering a plane incident wave by a
periodic surface. We will here consider the case, when the total
field vanishes on the surface. This corresponds, for example, to a TE polarised
electromagnetic wave incident onto a perfectly conducting surface. 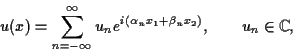
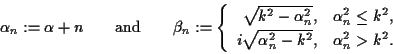
 A further consequence of these assumptions is that the problem can be formulated
equivalently through a boundary integral equation that only involves an integral over
a single period and thus is finite. Thus the corresponding integral operator can
be shown to be compact.
A further consequence of these assumptions is that the problem can be formulated
equivalently through a boundary integral equation that only involves an integral over
a single period and thus is finite. Thus the corresponding integral operator can
be shown to be compact.